Competencia: Desarrollo de Software (Nivel 2)
Palabras Clave: BlueJ, Java, Integrales, area.
Trabajar en BlueJ una solución que permita encontrar el área bajo una curva, haciendo las máximas pero optimas particiones posibles.
para esta actividad primero debíamos tener claro, como funciona el método del trapecio.
Regla del trapecio
En matemática la regla del trapecio es un método de integración numérica, es decir, un método para calcular aproximadamente el valor de la integral definida
La regla se basa en aproximar el valor de la integral de f(x) por el de la función lineal que pasa a través de los puntos (a, f(a)) y (b, f(b)). La integral de ésta es igual al área del trapecio bajo la gráfica de la función lineal. Se sigue que
y donde el término error corresponde a:
Siendo ξ un número perteneciente al intervalo [a,b].
nuestro programa tenia la misión de repetirse tantas veces como fuese necesario hasta encontrar un epsilon mínimo,
lo cual nos diría que las particiones son suficientes.
CÓDIGO:
Este trabajo nos mostró, que muchas veces no es necesario tener un conocimiento profundo de un área,
a veces distinta a la que estamos acostumbrados a trabajar, pero si importa tener claro cual es el objetivo al que se apunta y a que problema se quiere encontrar solución.
vimos también que un programa recursivo, nos ahorra muchísimo tiempo en cálculos muchas veces simples pero tediosos, y hacerlo con un exactitud total.

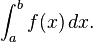
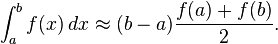



No hay comentarios:
Publicar un comentario